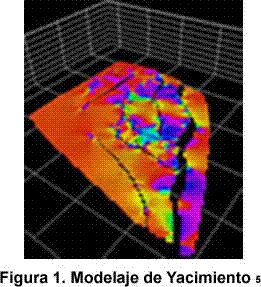
Simulación Geoestadística: Métodos del tipo Gaussiano
Este método de simulación Geoestadistico del tipo Gaussiano requiere que la función distribución de probabilidad (FDP) multivariada de una funcion aleatoria Z(x) sea Gaussiana , Esta función aleatoria Z (x) puede ser caracterizada por una función de distribución de probabilidad y, en dependencia de su grado de estacionaridad, por una función de correlación (función de covarianzas o semivarianzas).
Existen muchas dificultades a la hora de hacer la simulación una de ellas es debido a que casi ningun fenómeno de la ciencia se ajusta a un histogramas simetricos y mucho menos a Gaussianos. Como se sabe se necesitan muchas condiciones necesarias para que una funcion aleatoria sea una distribución normal multivariada y una de ellas es que su distribución univariada sea normal, para eso se necesita transformar a la funcion Z(x) de manera que resulte su función distribución de probabilidad (FDP) normal.
Para transformarlo a una funcion normal se debe hacer de la siguiente manera:
Si Y(x) es una funcion aleatoria con la función distribución de probabilidad (FDP) univariada Fy (y)=G(y) normal estandarizada N(0,1) para lo cual se debe cumplir que;

y por lo tanto la transformación que se requiere sería;

En la práctica los n datos de la muestra de Z (x) son ordenados de modo creciente de sus valores:


la función distribución de probabilidad (FDP) de Z(x) esta dada por


A este tipo de transformación se le conoce como anamorfosis.
Pero esto aún sería insuficiente puesto que se requeriría verificar la normalidad al menos de la distribución bivariada. Aunque en muchos casos para fines prácticos no se lleva tan lejos el análisis y se toma la decisión de considerar a la distribución gaussiana o por el contrario se rechaza esa hipótesis y se elige otro método de simulación no gaussiano.
Luego de realizar la simulación Gaussiana a los datos transformados se requiere hacer la transformación inversa de los valores simulados obtenidos. En la Fig. 6.1 se muestra un esquema general de cómo proceder con las simulaciones de tipo Gaussianas.