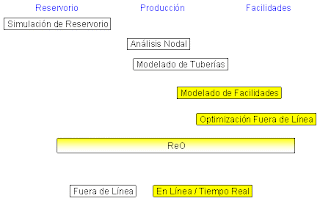
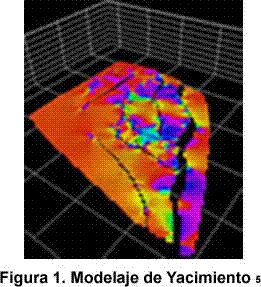
Análisis de Simulación para interacción pozos Productores-Inyectores

El petróleo pesado no tiene habilidad para salir por si mismo de los poros de la roca del yacimiento en los cuales se encuentra, más bien sale por el empuje que puede generar la acumulación de un fluido inmiscible, como lo es el agua. A este proceso se le conoce como desplazamiento de fluidos inmiscibles.

A medida que se inyecta el primero, se va formando un frente de separación y se comienzan a distinguir dos regiones en el medio poroso: una que contiene principalmente petróleo con agua connata o irreducible, y la otra que contiene principalmente agua con petróleo residual o inmóvil (1).

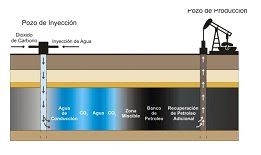
Desplazamiento Inmiscible de fases

Para maximizar el recobro en estos yacimientos es necesario cuantificar el volumen de fluido que se requiere inyectar en el medio poroso.

El recobro esta regido por la extensión de fluido desplazante, el cual desplaza al petróleo y satura los poros del yacimiento. El modelaje de cualquier proceso de recobro requiere un amplio conocimiento de las permeabilidades del sistema agua-petróleo-roca. Las permeabilidades relativas se pueden determinar por el método de flujo en estado estable (conocido como Penn-State) y el método de flujo en estado no-estable, el cual usa la teoría de desplazamiento de Buckley-Leverett. La permeabilidad relativa es usualmente expresada como función de la saturación de la fase fluyente pero esta relación se ve alterada por varios factores como las viscosidades y las tensiones interfaciales entre el fluido desplazante y desplazado. Los efectos de estos factores están ligados y correlacionados como una función del número de capilaridad definida como:

Estudios reportaron que la Sor disminuye significativamente con el aumento de Nc.

El método de la solución característica a la ecuación de flujo unidimensional de Buckley-Leverett es usado para investigar los efectos de varios parámetros, como la razón de movilidad y el volumen de fluido inyectado requerido antes de alcanzar la saturación de petróleo residual (Sor).

Estos experimentos consideraron el flujo unidimensional de fluidos inmiscibles e incompresibles, despreciando los esfuerzos de las fuerzas capilares y gravitacionales, y tomando en cuenta la distribución de saturaciones detrás del frente de saturación. Para los sistemas de desplazamiento de petróleo pesado con agua, donde la diferencia de densidades se aproxima a cero (ρw – ρo ≈ 0). Para este proceso de desplazamiento de un fluido viscoso por otro menos viscoso, la razón de movilidad es adversa, por lo cual se espera que exista discontinuidad en la distribución de saturación. Entonces se genera la siguiente ecuación simplificada:

Luego del desarrollo de la ecuación diferencial se llega a la siguiente ecuación:

Con la cual es posible calcular el máximo volumen poroso (PV) de fluido a inyectar, garantizando el máximo recobro de petróleo pesado.

Sin embargo, para el proceso de simulación estas ecuaciones y suposiciones son soluciones bases para el calculo y formulación posterior, acerca de estas formulaciones hay especificaciones en la referencia 2.

Resultados Obtenidos en estudios comparativos se muestran a continuación (2):

Caso 1. Simulador Bifásico Bidimensional del Desplazamiento de Petróleo por Agua (2)

Se desarrolló un simulador bifásico -agua-petróleo- bidimensional, incompresible que modela un proceso de recuperación secundaria de petróleo mediante inyección de agua. Unas de las ejemplificaciones es el simulador representa un esquema de cinco puntos invertido, que consiste en una malla cuadrada con un inyector en el centro y cuatro productores en los vértices. El simulador puede aplicarse a simular la porción de reservorio afectada al esquema de cinco puntos, ensayos piloto en campo o ensayos de desplazamiento de petróleo por agua, realizados en una celda experimental de laboratorio. Para resolver numéricamente el sistema de ecuaciones diferenciales parciales no lineales que rige el flujo bifásico, se aplica una técnica en diferencias finitas, el método de Soluciones Simultáneas.

El sistema de ecuaciones que representa el flujo bifásico agua-petróleo incompresible, a través de un medio poroso bidimensional en coordenadas cartesianas surge de combinar la ecuación de conservación de la masa con la ecuación de movimiento de Darcy para cada fase (Thomas, 1982). Las incógnitas del sistema son las presiones y saturaciones de ambas fases.

El sistema resulta no lineal, ya que como coeficientes de las ecuaciones diferenciales aparecen las curvas de permeabilidades relativas agua-petróleo, que son funciones de las saturaciones. Se elige un método en diferencias finitas, basado en una formulación implícita, el método de Soluciones Simultáneas. La necesidad de desarrollar un simulador incompresible surge pues los simuladores convencionales trifásicos presentan problemas al considerar nulas las compresibilidades de los fluidos (Aziz and Settari, 1985). Por ejemplo, las formulaciones semi-implícitas, como IMPES (Implícito en Presión, Explícito en Saturación), presentan problemas de singularidad del sistema de ecuaciones algebraicas resultante de la discretización.

Para realizar la simulación numérica se define una grilla cuadrada con una cantidad impar de nodos. A las ecuaciones expresadas en términos de presión se les aplica un esquema en diferencias finitas atrasado en el tiempo y centrado en el espacio. Se obtiene así un sistema de ecuaciones algebraicas no-lineales. El sistema se resuelve linealizando en distintas etapas pero cuya idea básica es nuevamente aplicar el cambio de variables de saturación a presión capilar.

Las formulaciones matemáticas pueden ser observadas en el trabajo de investigación mencionado.

Caso2. Otros modelos estudiados La Simulación Numérica Dinámica en Líneas de Flujo (SNDLF) constituye una alternativa innovadora que permite el manejo de Modelos Dinámicos en una escala “fina” (sin Upscaling) ya que, al desacoplar la geometría y la heterogeneidad del flujo de las ecuaciones de transporte, resultan computacionalmente rápidos y eficientes en la resolución de problemas dominados por flujos convectivos (sistemas no altamente compresibles) (3).

La Simulación en Líneas de Flujo comienza resolviendo las ecuaciones de flujo mediante la obtención del campo tridimensional de Presiones considerando las propiedades de las rocas, fluidos y condiciones de contorno. Posteriormente, se trazan las Líneas de Flujo siguiendo el gradiente de Presiones, en forma tangencial al campo vectorial de velocidad total, y plantea la ecuación de transporte de fluidos, aplicando la Ley de Darcy correspondiente, a lo largo de la Línea de Flujo en forma unidimensional. Para ello sustituye en esa ecuación las variables x, y, z por una variable τ, llamada Tiempo de Vuelo (TOF), que representa el tiempo que un trazador neutral requiere para alcanzar un punto “s” de la Línea de Flujo. De esta forma las líneas de flujo dejan de ser tan sensibles a la forma y tamaño de los bloques. A continuación se resuelve un Balance de Masa en cada Línea de Flujo para mover la composición del fluido en el tiempo, se mapea esa composición a lo largo de cada línea y finalmente se distribuye el fluido en la vertical considerando el efecto gravitatorio y volviéndolo a mapear en la grilla 3D. Así, automáticamente, se vuelve a comenzar el ciclo resolviendo el campo de presiones en cada paso temporal deseado. Todo este proceso de simulación es rápido, lo que permite tener una gran discretización espacial, y por lo tanto, representar en mayor medida la heterogeneidad de los reservorios de manera más cercana a la realidad (3).

Referencias

1. V. Reitman, V.S.V. Rajan, T.R. Heidrick, “The effect of inyected fluid Volume on Heavy Oil Displacement in a Porous Medium”. Paper SPE 15065, presented at the 56th California Regional Meeting of the Society of Petroleum Engineers April, 1986

2. María de los Á. Morellia, Marina L. Fusarib y Gabriela B. Saviolib, “Simulador Bifásico Bidimensional del Desplazamiento de Petróleo por Agua” Mecánica Computacional Vol XXV, pp. 2633-2647, Santa Fe, Argentina, Noviembre 2006

3. MIRTA GALACHO, NÉSTOR GALACHO, PABLO VÁZQUEZ Y LUCIANA MASUD, “Mallas de Recuperación Secundaria Optimización del Diseño por Simulación en Líneas de Flujo” MG&A OIL & GAS, presentado por primer Congreso iNNotec, septiembre de 2004 en Buenos Aires, Argentina