SIMULACIÓN NUMÉRICA DE YACIMIENTOS. (Parte V)
CONSTRUCCIÓN DE LA MALLA DE SIMULACIÓN.
CARACTERÍSTICAS NUMÉRICAS.
La selección del tamaño y la orientación de la malla también dependen de algunas características numéricas, siendo las más importantes las asociadas a la dispersión numéricas y efectos de orientación de la malla.
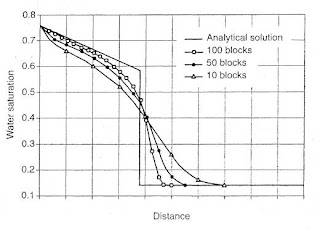
Fig. 1 – Efecto de la dispersión numérica
La dispersión numérica es un artificio de las técnicas numéricas actuales, la cual ocurre en los procesos de simulación asociados a cambios rápidos en la saturación de agua y petróleo en procesos de imbibición. La dispersión numérica introduce un sesgo en los resultados, el cual está relacionado a las dimensiones de las celdas que son usadas en el modelo de simulación.
La Fig. 1 ilustra el problema. Cuando el mismo proceso de desplazamiento es simulado usando un número de celdas diferentes, el perfil de saturaciones cambia. Como se puede notar, el efecto de la dispersión numérica es alterar negativamente el perfil de saturaciones cuando se usan pocas celdas y por lo tanto decrece la eficiencia del desplazamiento en el avance. Además, este efecto es más pronunciado en la presencia de una relación de movilidades favorable.
La dispersión numérica está siempre presente en cualquier modelo de simulación en aluna medida, aunque reducir el tamaño de las celdas minimiza el impacto en el cálculo de los resultados. Se debería buscar un balance satisfactorio en la selección de las dimensiones de la malla, para limitar el efecto de la dispersión numérica y trabajar con un número de celdas práctico.
Los efectos de la orientación de la malla, por otro lado, refieren un sesgo en los resultados calculados, los cuales se derivan de la orientación de la malla con respecto a la posición de los pozos productos e inyectores. El problema esta ilustrado en la Fig. 2, donde se muestran 2 pozos inyectores y 1 productor, nombrados A, B y C respectivamente. Usando el mallado en la figura, el camino del inyector B al productor C es mucho más largo que el camino del inyector A, por lo tanto el tiempo de avance puede ser artificialmente más largo. Se tiene en cuenta que rotar la cuadrícula 45 grados revertiría la situación.

Fig. 2 – Efectos de la orientación de la malla
Los efectos por orientación en la malla particularmente importan en la presencia de altas relaciones de movilidad, como en el caso de procesos de desplazamiento gas-petróleo o vapor-petróleo, pero este impacto no debería ser pasado por alto, ni siquiera en los sistemas más convencionales agua-petróleo. La solución más efectiva para limitar los efectos de la orientación de la malla es posiblemente el uso de “nueve puntos” en la formulación de la ecuación de flujo, donde las conexiones diagonales también están tomadas en cuenta (Fig. 3). Este enfoque es más intensivo computacionalmente, sin embargo cuando el tiempo de computación no es un problema, el esquema de los “nueve puntos” debería ser la opción preferida.

Fig. 3 – Esquema de computación de: cinco puntos (A) vs. nueve puntos (B)
Fuente:
Cosentino Luca, (2001). Integrated Reservoir Studies, Institut Francais Du Pétrole Publications, Editions TECHNIP.